扩散模型(Diffusion Model)

主要针对扩散模型的一些经典文章写一些个人理解,博采众长,参考了很多博客、文章,详细信息见参考文献
Table of Contents
0、文生图片模型
- DALL·E 3
扩散模型的大火始于2020年所提出的DDPM(“Denoising Diffusion Probabilistic Models”)。当前最先进的两个文本生成图像——OpenAI的DALL·E 3和Google的Imagen 2,都是基于扩散模型来完成的。
1、几种生成模型的对比
-
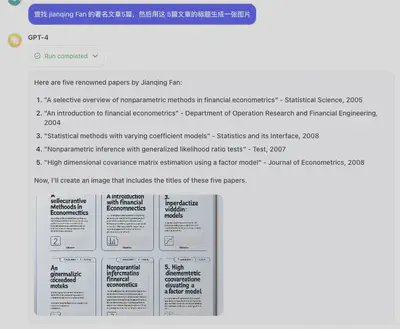
GAN(生成对抗网络):GAN是由两部分组成,一个生成器和一个判别器。生成器的目标是创建足够真实的数据,以至于判别器不能区分生成的数据和真实数据。判别器的目标是正确区分真实数据和生成器生成的假数据。这两部分在训练过程中相互竞争,推动彼此的进步,因此称为对抗网络。GAN在图像生成方面尤其出色。
-
VAE(变分自编码器):VAE采用不同的方法来生成数据。它通过编码器将数据映射到一个分布上,并从这个分布中采样来构造一个解码器用于数据重建。它是一种通过概率方法生成新数据的模型,通常用于生成遵循特定统计分布的图片。
-
Flow-based Models(基于流的模型):这类模型使用可逆变换来学习数据的分布,这意味着它们可以精确地计算生成数据的概率。它们可以生成高质量的数据,并且给定新数据,也可以确定其概率。这种特性在密度估计和无损压缩方面特别有用。
-
Diffusion Models(扩散模型):Diffusion Models 的灵感来自non-equilibrium thermodynamics (非平衡热力学)。理论首先定义扩散步骤的马尔可夫链,以缓慢地将随机噪声添加到数据中,然后学习逆向扩散过程以从噪声中构造所需的数据样本。与 VAE 或流模型不同,扩散模型是通过固定过程学习,并且隐空间具有比较高的维度。
2、扩散模型(DDPM)
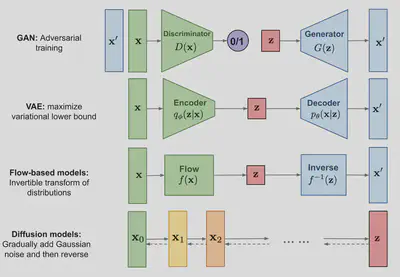
考虑下图瑞士卷形状的二维联合概率分布$p(x,y)$,扩散过程$q$非常直观,本来集中有序的样本点,受到噪声的扰动,向外扩散,最终变成一个完全无序的噪声分布

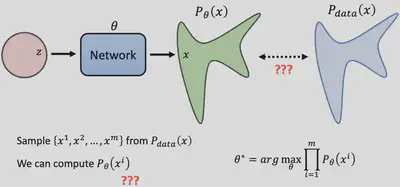
2.1 Diffusion Model原理
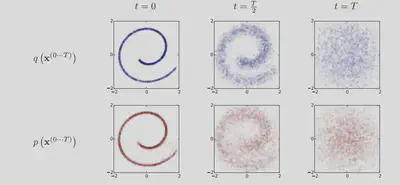
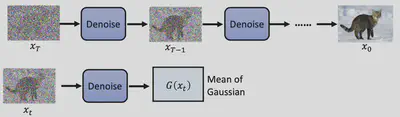
Diffusion Models由正向过程(或扩散过程)和反向过程(或逆扩散过程)组成:
-
逆向过程(Inverse Process)
-
正向过程(Forward Process)

原文算法框

Denoise Module
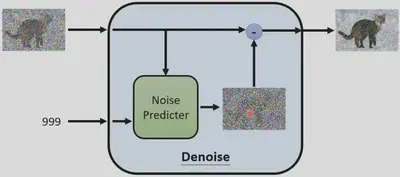
如何训练
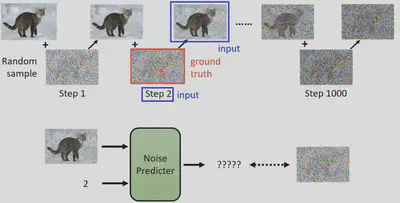
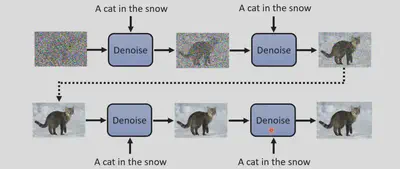
如何从文本生成图片

2.2 DDPM 数学推导

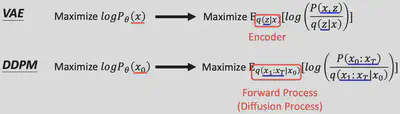
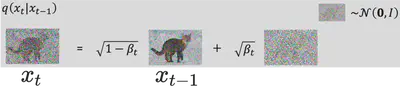

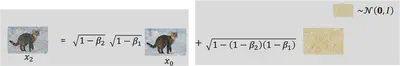
$$
\begin{aligned}
& \log p(\boldsymbol{x}) \geq \mathbb{E}_{q\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right)}\left[\log \frac{p\left(\boldsymbol{x}_{0: T}\right)}{q\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right)}\right] \\
& =\mathbb{E}_{q\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right)}\left[\log \frac{p\left(\boldsymbol{x}_T\right) \prod_{t=1}^T p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)}{\prod_{t=1}^T q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_{t-1}\right)}\right] \\
& =\mathbb{E}_{q\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right)}\left[\log \frac{p\left(\boldsymbol{x}_T\right) p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_0 \mid \boldsymbol{x}_1\right) \prod_{t=2}^T p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)}{q\left(\boldsymbol{x}_1 \mid \boldsymbol{x}_0\right) \prod_{t=2}^T q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_{t-1}\right)}\right] \\
& =\mathbb{E}_{q\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right)}\left[\log \frac{p\left(\boldsymbol{x}_T\right) p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_0 \mid \boldsymbol{x}_1\right) \prod_{t=2}^T p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)}{q\left(\boldsymbol{x}_1 \mid \boldsymbol{x}_0\right) \prod_{t=2}^T q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_{t-1}, \boldsymbol{x}_0\right)}\right] \\
& =\mathbb{E}_{q\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right)}\left[\log \frac{p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_T\right) p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_0 \mid \boldsymbol{x}_1\right)}{q\left(\boldsymbol{x}_1 \mid \boldsymbol{x}_0\right)}+\log \prod_{t=2}^T \frac{p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)}{q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_{t-1}, \boldsymbol{x}_0\right)}\right] \\
& =\mathbb{E}_{q\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right)}\left[\log \frac{p\left(\boldsymbol{x}_T\right) p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_0 \mid \boldsymbol{x}_1\right)}{q\left(\boldsymbol{x}_1 \mid \boldsymbol{x}_0\right)}+\log \prod_{t=2}^T \frac{p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)}{\frac{q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right) q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_0\right)}{q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_0\right)}}\right] \\
& =\mathbb{E}_{q\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right)}\left[\log \frac{p\left(\boldsymbol{x}_T\right) p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_0 \mid \boldsymbol{x}_1\right)}{q\left(\boldsymbol{x}_1 \mid \boldsymbol{x}_0\right)}+\log \prod_{t=2}^T \frac{p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)}{\frac{q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right) q\left(\boldsymbol{x}_t+\boldsymbol{x}_0\right)}{q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_0\right)}}\right] \\
& =\mathbb{E}_{q\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right)}\left[\log \frac{p\left(\boldsymbol{x}_T\right) p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_0 \mid \boldsymbol{x}_1\right)}{q\left(\boldsymbol{x}_1 \mid \boldsymbol{x}_0\right)}+\log \frac{q\left(\boldsymbol{x}_1 \mid \boldsymbol{x}_0\right)}{q\left(\boldsymbol{x}_T \mid \boldsymbol{x}_0\right)}\right.\\
&~~~~~~~~~~~~~~~~~~~~~~~~+\left.\log \prod_{t=2}^T \frac{p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)}{q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right)}\right] \\
& =\mathbb{E}_{q\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right)}\left[\log \frac{p\left(\boldsymbol{x}_T\right) p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_0 \mid \boldsymbol{x}_1\right)}{q\left(\boldsymbol{x}_T \mid \boldsymbol{x}_0\right)}+\sum_{t=2}^T \log \frac{p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)}{q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right)}\right] \\
& =\mathbb{E}_{q\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right)}\left[\log p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_0 \mid \boldsymbol{x}_1\right)\right]+\mathbb{E}_{q\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right)}\left[\log \frac{p\left(\boldsymbol{x}_T\right)}{q\left(\boldsymbol{x}_T \mid \boldsymbol{x}_0\right)}\right]\\
& ~~~~~~~~~ \qquad \qquad +\sum_{t=2}^T \mathbb{E}_{q\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right)}\left[\log \frac{p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)}{q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right)}\right] \\
& =\mathbb{E}_{q\left(\boldsymbol{x}_1 \mid \boldsymbol{x}_0\right)}\left[\log p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_0 \mid \boldsymbol{x}_1\right)\right]+\mathbb{E}_{q\left(\boldsymbol{x}_T \mid \boldsymbol{x}_0\right)}\left[\log \frac{p\left(\boldsymbol{x}_T\right)}{q\left(\boldsymbol{x}_T \mid \boldsymbol{x}_0\right)}\right]\\
& ~~~~~~~~~ \qquad \qquad +\sum_{t=2}^T \mathbb{E}_{q\left(\boldsymbol{x}_t, \boldsymbol{x}_{t-1} \mid \boldsymbol{x}_0\right)}\left[\log \frac{p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)}{q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right)}\right] \\
& =\underbrace{\mathbb{E}_{q\left(\boldsymbol{x}_1 \mid \boldsymbol{x}_0\right)}\left[\log p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_0 \mid \boldsymbol{x}_1\right)\right]}_{\text {reconstruction term }}-\underbrace{D_{\mathrm{KL}}\left(q\left(\boldsymbol{x}_T \mid \boldsymbol{x}_0\right) \| p\left(\boldsymbol{x}_T\right)\right)}_{\text {prior matching term }}\\
& ~~~~~~~~~ \qquad \qquad -\sum_{t=2}^T \underbrace{\mathbb{E}_{q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_0\right)}\left[D_{\mathrm{KL}}\left(q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right) \| p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)\right)\right]}_{\text {denoising matching term }}
\end{aligned}
$$
因此,我们得到了DDPM中$\log P(x)$的lower bound:
$$
\begin{aligned}
&\mathrm{E}_{q\left(x_1 \mid x_0\right)}\left[\log P\left(x_0 \mid x_1\right)\right] -K L\left(q\left(x_T \mid x_0\right)|| P\left(x_T\right)\right) \\
& ~~~ \qquad -\sum_{t=2}^T \mathrm{E}_{q\left(x_t \mid x_0\right)}\left[K L\left(q\left(x_{t-1} \mid x_t, x_0\right)\| P\left(x_{t-1} \mid x_t\right)\right)\right]
\end{aligned}
$$
我们并不需要计算$K L\left(q\left(x_T \mid x_0\right)|| P\left(x_T\right)\right)$,因为这里的$P\left(x_T\right)$是从高斯分布中采样,而$q\left(x_T \mid x_0\right)$是我们人为设定的 diffusion process,这两个分布均于神经网络参数$\theta$无关,可以视为一个常数。我们重点关注的应该是最后一项$\sum_{t=2}^T \mathrm{E}_{q\left(x_t \mid x_0\right)}\left[K L\left(q\left(x_{t-1} \mid x_t, x_0\right)\| P\left(x_{t-1} \mid x_t\right)\right)\right]$,至于第一项,优化的思路类似于最后一项,这里不再展开,详细的情况可以参看原论文或(Diffusion Models:生成扩散模型-知乎)。对于$\sum_{t=2}^T \mathrm{E}_{q\left(x_t \mid x_0\right)}\left[K L\left(q\left(x_{t-1} \mid x_t, x_0\right)\| P\left(x_{t-1} \mid x_t\right)\right)\right]$这一项,难点在于计算$q\left(x_{t-1} \mid x_t, x_0\right)$,由于我们可以计算$q\left(x_{t} \mid x_0\right)$, $q\left(x_{t-1} \mid x_0\right)$以及$q\left(x_{t} \mid x_{t-1}\right)$:
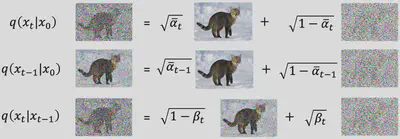

既然$q\left(x_{t-1} \mid x_t, x_0\right)$与$P\left(x_{t-1} \mid x_t\right)$均为高斯分布,那么KL散度是有显示解的,即: $$ \begin{aligned} & D_{\mathrm{KL}}\left(\mathcal{N}\left(\boldsymbol{x} ; \boldsymbol{\mu}_x, \boldsymbol{\Sigma}_x\right) | \mathcal{N}\left(\boldsymbol{y} ; \boldsymbol{\mu}_y, \boldsymbol{\Sigma}_y\right)\right)\\ =&\frac{1}{2}\left[\log \frac{\left|\boldsymbol{\Sigma}_y\right|}{\left|\boldsymbol{\Sigma}_x\right|}-d+\operatorname{tr}\left(\boldsymbol{\Sigma}_y^{-1} \boldsymbol{\Sigma}_x\right)+\left(\boldsymbol{\mu}_y-\boldsymbol{\mu}_x\right)^T \boldsymbol{\Sigma}_y^{-1}\left(\boldsymbol{\mu}_y-\boldsymbol{\mu}_x\right)\right] \end{aligned} $$
但是我们有更简单的方法来替代KL散度的计算,具体而言,我们注意到$q\left(x_{t-1} \mid x_t, x_0\right)$是一个跟网络参数无关的高斯分布,因此其均值和方差都是固定的,而$P\left(x_{t-1} \mid x_t\right)$中,我们会控制 Denoise 的方差,但是其均值是更网络参数有关的,因此我们只需要让这两个分布的均值接近就可以,这就等价于最小化KL散度
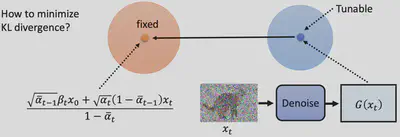
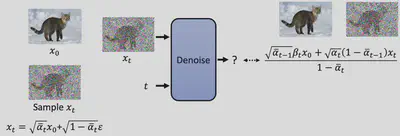
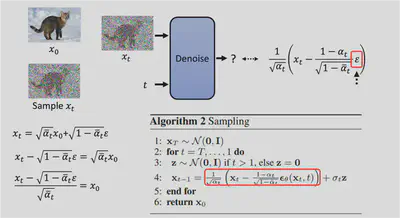
最后,我们注意到算法二中Sampling的公式
$$
\mathbf{x}_{t-1}=\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\right)+{\color{red}{\sigma_t \mathbf{z}}}
$$
仍然在每一步引入了随机项,为什么不直接取均值呢?这个问题其实跟文本生成模型中引入随机性是一样的道理,如下图所示,在文本生成模型中,如果每次都取概率最大的,那么生成的文字很有可能出现重复进而导致较差的效果:


3 、基于分数的生成模型(Score-based generative models)
主要参考:知乎:@CW不要無聊的風格
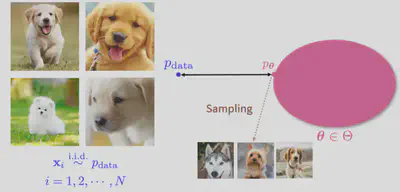
3.1 朗之万动力学采样
朗之万动力学(Langevin dynamics)是物理学中对分子系统进行统计建模(布朗运动)的工具

上图模拟了花粉(黄色)收到大量水分子的撞击进行随机的布朗运动的情形。朗之万方程可化简为
$${X_{t+dt}} = X_t-\frac{dt}{\gamma} \frac{\partial E}{\partial X}+\frac{dt}{\gamma} \epsilon,$$ 这里的$-\frac{dt}{\gamma} \frac{\partial E}{\partial X}$表示能量减小得最快的方向,因此该方程刻画了粒子会往能量减小的最快的方向移动。而在2011年的文章Bayesian learning via stochastic gradient Langevin dynamics中,提出了随机梯度朗之万动力学,而基于分数的生成模型的一些理论保证就来源于该文章。那我们应该怎么使用这个动力学方程从一个分布$p(x)$进行采样呢?答案是下面这个公式:
$$
\tilde{\mathbf{x}}_t=\tilde{\mathbf{x}}_{t-1}+\frac{\epsilon}{2} \nabla_{\mathbf{x}} \log p\left(\tilde{\mathbf{x}}_{t-1}\right)+\sqrt{\epsilon} \mathbf{z}_t
$$
具体而言,我们可以从任意的先验分布$\pi(\mathbf{x})$中抽样一个初始样本$\tilde{\mathbf{x}}_0$,然后按照上式更新即可。这里的$\mathbf{z}_t\sim \mathcal{N}(0,I)$。因此我们可以发现这样的采样过程只会涉及到对数似然的梯度$\nabla_{\mathbf{x}} \log p\left(\tilde{\mathbf{x}}_{t-1}\right)$,只要我们能准确地近似这个梯度,那么我们就可以随意采样,随意生成高质量的图片。这个梯度被称之为“分数”(score),这也是该类方法的名字由来。理论上, 在一定约束条件下, 并且当 $\epsilon \rightarrow 0, T \rightarrow \infty$ 时, 最终生成的样本 $x_T$ 将会服从原数据分布 $p_{\text {data }}(x)$ 。
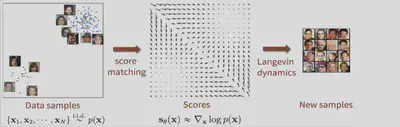
因此,现在的问题转化为如何利用神经网络得到$\mathbf{s}_\theta(\mathbf{x})$,使其约接近$\nabla_{\mathbf{x}} \log p\left(\tilde{\mathbf{x}}_{t-1}\right)$越好
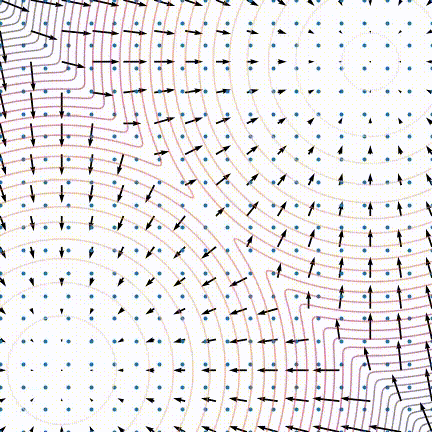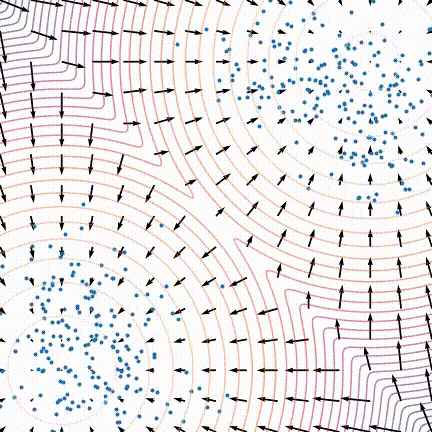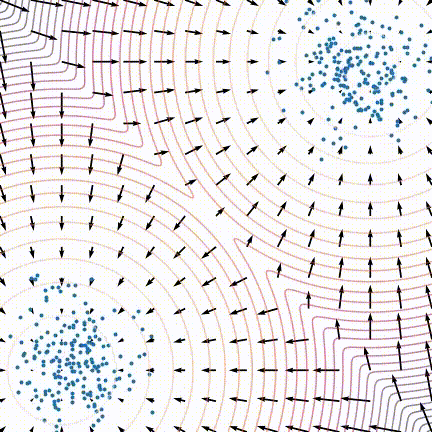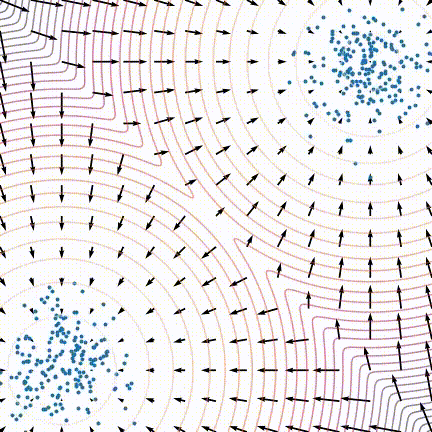
3.2 分数模型理论
根据前面的介绍,我们可以得到分数模型的训练目标 $$ \frac{1}{2} E_{p_{\text {data }}}\left[\left\|s_\theta(x)-\frac{\partial \log \left(p_{\text {data }}(x)\right)}{\partial x}\right\|_2^2\right]\qquad (1) $$ 其中, $\theta$代表网络参数,$s_\theta(x)$是网络估计的分数,其减去的右边那项代表真实的分数,$E_{P_{d a t a}}$表示在整体数据中求期望。但是这显示是无法计算的,因为我们并不知道分布$p_{\text {data }}$,但是我们可以通过score matching(分数匹配) 的方法,可以让我们在不了解概率密度的情况下也可以成功训练出模型来估计分数,即上述目标函数等价于
$$ \mathbb{E}_{p_{\text {data }}(\mathbf{x})}\left[\operatorname{tr}\left(\nabla_{\mathbf{x}} \mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x})\right)+\frac{1}{2}\left\|\mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x})\right\|_2^2\right] $$ 这里的$\nabla_{\mathbf{x}} \mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x})$其实就是 Jacobian矩阵,但是注意到当$\mathbf{x}$维度很高的时候,$\nabla_{\mathbf{x}} \mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x})$的反向传播是非常麻烦的,因此论文中提到了两种方法来解决这个问题,分别是:sliced score matching和denoising score matching
- Sliced Score Matching(切片分数匹配)
既然这个矩阵的trace很难计算,那我们可以尝试去估计它,利用Hutchinson trace estimator,对于任意一个矩阵$A$,我们有 $$ \begin{aligned} \operatorname{tr}(A)&=\operatorname{tr}\left(A \mathbb{E}\left[v v^T\right]\right)=\operatorname{tr}\left(\mathbb{E}\left[A v v^T\right]\right)=\mathbb{E}\left[\operatorname{tr}\left(A v v^T\right)\right]\\ &=\mathbb{E}\left[\operatorname{tr}\left(v^T A v\right)\right]=\mathbb{E}\left[v^T A v\right] \end{aligned} $$ 其中$v\sim (0,I)$,因此我们可以得到
$$\operatorname{tr}\left(\frac{\partial s_\theta(x)}{\partial x}\right)=\mathbb{E}_{p_v}\left[v^T \frac{\partial s_\theta(x)}{\partial x} v\right]=\mathbb{E}_{p_v}\left[\frac{\partial\left(v^T s_{\theta(x)}\right)}{\partial x} v\right]$$ 这样就很大程度上简化了梯度的计算,训练的目标函数也变为: $$ E_{p_v} E_{p_{\text {data }}}\left[\frac{\partial\left(v^T s_\theta(x)\right)}{\partial x} v+\frac{1}{2}\left\|s_\theta(x)\right\|_2^2\right] $$
- Denoising Score Matching(去噪分数匹配)
这个方法是原文默认的方法,具体而言,就是在原分布上加噪声,然后利用$(1)$式来训练。记训练样本为 $x$, 加噪后的数据为 $\tilde{x}$, 预定义的分布为 $q_\sigma(\tilde{x} \mid x) \sim N\left(\tilde{x} ; x, \sigma^2 I\right)$, 方差 $\sigma^2$ 预先定义好。加噪后的数据分布表示为: $q_\sigma(\tilde{x})=\int q_\sigma(\tilde{x} \mid x) p_{\text {data }}(x) d x$。
$$ \begin{aligned} &\mathbb{E}_{q_\sigma(\tilde{x})}\left[\left\|s_\theta(\tilde{x})-\frac{\partial \log \left(q_\sigma(\bar{x})\right)}{\partial \tilde{x}}\right\|^2\right]\\ =&\mathbb{E}_{q_\sigma(\tilde{x} \mid x) p_{\text {data }}(x)}\left[\left\|s_\theta(\tilde{x})-\frac{\partial \log \left(q_\sigma(\tilde{x} \mid x)\right)}{\partial \tilde{x}}\right\|^2\right]+C \end{aligned} $$ 其中$C$为一个与模型参数$\theta$不相关的常数项。
等号左边是加噪后最直接的分数匹配形式(显式的分数匹配(Explicit Score Matching)),而等号右边则是实际使用的去噪分数匹配形式(DSM),ESM与DSM的等价性证明见(知乎)。于是, 训练目标就转化为: $$ \frac{1}{2} E_{q_\sigma(\tilde{x} \mid x) p_{\text {data }}(x)}\left[\left\|s_\theta(\tilde{x})-\frac{\partial \log \left(q_\sigma(\tilde{x} \mid x)\right)}{\partial \tilde{x}}\right\|_2^2\right] $$ 在训练模型时,我们只需要将加噪后的样本$\tilde{x}$喂给模型即可计算估计分数,但是另外, 这个分数是对应噪声数据分布$q_\sigma(\tilde{x})$的, 而非原始数据分布$p_{\text {data }}(x)$,因此我们需要让$q_\sigma(\tilde{x})$尽可能与$p_{\text {data }}(x)$ 接近, 这就要求预定义的$\sigma$ 要足够小。否则, 如果对原始数据扰动过大,模型训练完后生成的样本就会严重偏离原数据分布。
3.3 分数模型面临的问题
- 训练时损失不收敛
基于sliced score matching方式下训练的loss
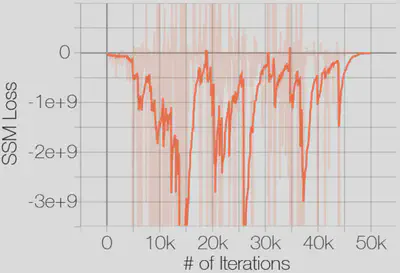
-
分数估计不准
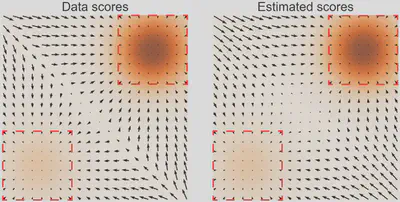
-
生成结果偏差大
原文中,作者发现训练后的模型生成效果不佳,采样生成出来的样本不太符合原数据分布。作者发现当数据分布是由多个分布按一定比例混合而成时,在朗之万动力学采样的玩法下,即使用真实的分数,采样生成出来的结果也可能不能反应出各个分布之间的比例关系,如下图所示:
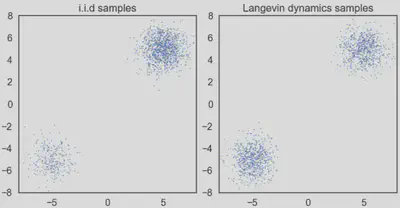
对于整体数据分布对应的分数, 如果我们分别来看其中两个分布对应的分数, 就会发现其实和它们的混合比例不相关: $$ \begin{aligned} \frac{\partial \log \left(p_{\text {data }}(x)\right)}{\partial x}=& \frac{\partial \log \left(\pi p_1(x)\right)}{\partial x}+\frac{\partial \log \left((1-\pi) p_2(x)\right)}{\partial x}\\ =&\frac{\partial \log \left(p_1(x)\right)}{\partial x} +\frac{\partial \log \left(p_2(x)\right)}{\partial x} \end{aligned} $$
这样就就没有关于$\pi$的信息了。原文说到面对这种混合分布的情况,从理论上来说,朗之万动力学采样是可以生成与原分布相似的结果的,但可能需要很小的步长(step size)以及非常大的步数(steps)才能做到。
3.4 利用NCSN解决三个问题
NCSN是Noise Conditional Score Networks的缩写,作者用NCSN 解决了上一节中提到的三个问题。
- 解决Loss不收敛
NCSN利用了高斯噪声去扰动数据(仅仅需要一个非常小的扰动),而高斯噪声是分布在整个编码空间的,因此,扰动后的数据能够有机会出现在整个编码空间的任意部分,从而避免了分数(score)没有定义(undefined)的情况,同时使得分数匹配公式适用,这就破解了“loss 不收敛”的困局。
- 解决分数估计不准
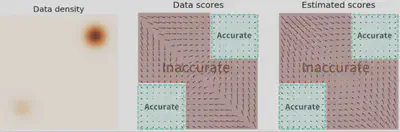

通过扰动数据的时候,噪声会有更多机会将原来的数据扩散到低概率密度区域,于是原来的低概率密度区域就能获得更多的监督信号,从而提升了分数估计的准确性,这就能破解了低密度趋于“分数估计不准”的问题。
- 解决生成结果偏差大
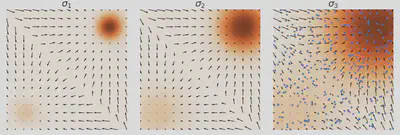
加噪后,原本“稀疏”的低概率密度区域就能够被“填满”,并且,自然地,两个分布中混合比例高的那个分布所占这部分(“填满”后的区域)的比例会更高,因此扰动后的分数将更多地由混合比例高的那个分布的分数“演变”而来。这就是说,分数的方向将更多地指向混合比例高的那个分布。
3.5 NCSN的技术细节
- 噪声设计原则
从前一节可以看出,加噪是该模型的精髓,但是具体应该加多大的噪声呢?直觉上为了让扰动后的分布能够更多地“填充”原来的低概率密度区域,我们应该加一个大的噪声,但是,我们需要用加噪后的分数 $\frac{\partial \log \left(q_\sigma(\tilde{x})\right)}{\partial \tilde{x}}$ 来近似原分布的分数 $\frac{\partial \log \left(p_{\text {data }}(x)\right)}{\partial x}$ 的 $(\tilde{x}, x$ 分别代表加噪后的数据与原数据)。若扰动过大, 抹去了原数据大部分信息, 就会造成近似效果不佳,因此噪声强度小能够获得与原数据分布较为近似的效果, 但是却不能够很好地“填充”低概率密度区域。于是,需要做一个 trade-off 。原文中,作者采用了一个噪声序列 $\left\{\sigma_i\right\}_{i=1}^L$, 并满足: $\frac{\sigma_1}{\sigma_2}=\ldots=\frac{\sigma_{L-1}}{\sigma_L}>1$, 同时 $\sigma_1$ 需要足够大, 以能够充分“填充”低概率密度区域; 而 $\sigma_L$ 得足够小, 以获得对原数据分布良好的近似, 避免过度扰动。
- 训练方法:去噪分数匹配
切片分数匹配(sliced score matching)也可以训练NCSN,但计算更多,训练过程会更慢,因此,作者使用去噪分数匹配进行训练,注意到我们的训练目标位
$$ \frac{1}{2} E_{q_\sigma(\tilde{x} \mid x) p_{\text {data }}(x)}\left[\left\|s_\theta(\tilde{x})-\frac{\partial \log \left(q_\sigma(\tilde{x} \mid x)\right)}{\partial \tilde{x}}\right\|_2^2\right] $$
由于加噪后的样本$\tilde{x}\sim\mathcal{N}(x,\sigma^2 \mathbf{I})$,因此
$$q_\sigma(\tilde{x} \mid x)=\frac{1}{\sqrt{2 \pi \sigma}} e^{-\frac{(\bar{x}-\mathrm{x})^2}{2 \sigma^2}}$$
将其取对数井对 $\tilde{x}$求导, 就可获得其分数的表示形式:
$$ \frac{\partial \log \left(q_\sigma(\bar{x} \mid x)\right)}{\partial \tilde{x}}=-\left(\frac{\bar{x}-x}{\sigma^2}\right) $$
将以上代入目标函数, 就得到在某个噪声级别 $\sigma$ 对应的损失函数:
$$ l(\theta ; \sigma) \equiv \frac{1}{2} E_{p_{\text {data }}(x)} E_{\tilde{x} \sim N\left(x, \sigma^2 I\right)}\left[\left|s_\theta(\tilde{x}, \sigma)+\frac{\bar{x}-x}{\sigma^2}\right|_2^2\right] $$
其中 $s_\theta(\tilde{x}, \sigma)$ 代表网络在特定噪声级别 $\sigma$ 下估计的分数。 而 NCSN 使用了多个噪声级别, 于是, 分别对它们的损失加权求和后再求均值, 就得到了联合的损失函数,它表示为:
$$ L\left(\theta ;\left\{\sigma_i\right\}_{i=1}^L\right) \equiv \frac{1}{L} \sum_{i=1}^L \lambda\left(\sigma_i\right) l\left(\theta ; \sigma_i\right) $$
其中$\lambda\left(\sigma_i\right)>0$代表不同噪声级别的损失的权重,但是应该怎么设置$\lambda\left(\sigma_i\right)$呢?首先需要保证的是加权后所有噪声级别的损失都在同一量级,不受$\sigma_i$ 的大小影响。然后作者 发现网络训练到收玫时, 估计出的分数的量级 $\left\|s_\theta(x, \sigma)\right\|_2$在 $\frac{1}{\sigma}$ 这个水平, 即: $s_\theta(x, \sigma) \asymp \frac{1}{\sigma}$ 。因此作者将 $\lambda(\sigma)$ 设置为 $\sigma^2$。其实,把$\lambda\left(\sigma_i\right)=\sigma_i^2$ 代入$L\left(\theta ;\left\{\sigma_i\right\}_{i=1}^L\right)$会发现:
$$ \begin{aligned} \lambda\left(\sigma_i\right) l\left(\theta ; \sigma_i\right)&=\sigma_i^2 l\left(\theta ; \sigma_i\right)=\frac{1}{2} E\left[\left\|\sigma_i s_\theta\left(\tilde{x}, \sigma_i\right)+\sigma_i \frac{\tilde{x}-x}{\sigma_i^2}\right\|_2^2\right] \\ & =\frac{1}{2} E\left[\left\|\sigma_i s_\theta\left(\tilde{x}, \sigma_i\right)+\frac{\tilde{x}-x}{\sigma_i}\right\|_2^2\right]\qquad(2) \end{aligned} $$
由于 $q_{\sigma_i}(\tilde{x} \mid x) \sim N\left(\tilde{x} ; x, \sigma_i^2 I\right)$, 因此有$\frac{\tilde{x}-x}{\sigma}$ 就是噪声 $\epsilon \sim N\left(0, I^2\right)$,这是与 $\sigma_i$ 无关的量, 即不受后者影响。在这种训练方式下, 只要预先设定好 $\left\{\sigma_i\right\}_{i=1}^L$, 然后在每次迭代时随机选取其中一个噪声级别 $\sigma_i$ , 并采样一个标准高斯噪声 $\epsilon$, 对原始数据样本加噪: $\tilde{x}=x+\sigma_i \epsilon$, 接着将加噪后的样本 $\tilde{x}$ 与对应的噪声级别 $\sigma_i$ 作为网络输入, 待其输出预测的分数 $s_\theta\left(\tilde{x}, \sigma_i\right)$ 后, 就可以使用 $(2)$ 来计算损失了。
- 采样生成:退火朗之万动力学

在训练好模型后,我们需要进行采样生成图片,原文中作者使用的方法为退火朗之万采样法,这种方法实质上是在噪声强度递减的情况下使用朗之万动力学采样,在每个噪声级别下都有一个朗之万动力学采样生成的过程。首先, 初始样本 $\tilde{x}_0$ 从某种固定的先验分布去采样(作者默认采用均匀分布); 然后, 从最大的噪声级别 $\sigma_1$ 开始使用朗之万动力学采样, 直至最小的噪声级别 $\sigma_L$ 。在每个噪声级别进行采样前, 会先设定步长(step size) $\alpha_i$,接着, 在每个噪声级别下, 基于一定的步数 $T$ 去迭代进行朗之万动力学采样。该噪声级别最后一步采样生成的样本会作为下一个噪声级别的初始样本(见上图 $\tilde{x}_0 \leftarrow x_T$); 最后, 待所有噪声级别的朗之万动力学采样过程均完成时, 就得到了最终的生成结果。这里步长设置的动机就是固定 “信噪比” (signalto-noise) 的量级,即$\frac{\alpha_i s_\theta\left(x, \sigma_i\right)}{2 \sqrt{\alpha_i} z}$ ( $z$ 是随机噪声)。该信噪比的量级为:
$$ E\left|\frac{\alpha_i s_\theta\left(x, \sigma_i\right)}{2 \sqrt{\alpha_i z}}\right|_2^2 \approx E\left[\frac{\alpha_i\left\|s_\theta\left(x, \sigma_i\right)\right\|_2^2}{4 z^2}\right] \asymp \frac{1}{4} E\left[\left\|\sigma_i s_\theta\left(x, \sigma_i\right)\right\|_2^2\right] $$
由于$s_\theta\left(x, \sigma_i\right) \asymp \frac{1}{\sigma_i}$, 于是这里就有 $\sigma_i s_\theta\left(x, \sigma_i\right) \asymp 1$ 。因此,我们得到 $\frac{1}{4} E\left[\left|\sigma_i s_\theta\left(x, \sigma_i\right)\right|_2^2\right] \asymp \frac{1}{4}$ 。这就说明, 在 $\alpha_i \asymp \sigma_i^2$ 的设置下, 信噪比会固定在常量级, 与噪声级别 $\sigma_i$ 无关。
3.6 DDPM和NCSN在SDE下的统一
主要参考知乎:@不许打针
宋飏大佬在 2021 年的ICLR的 best paper: Score-Based Generative Modeling through Stochastic Differential Equations中从 SDE(Stochastic Differential Equations)的角度说明了 NCSN 与 DDPM 在 SDE 的角度是一致的。
- 随机微分过程
许多随机过程(特别是扩散过程)都是随机微分方程 (SDE) 的解。一般来说, SDE具有以下形式:
$$ \mathrm{d} \boldsymbol{x}=f(\boldsymbol{x}, t) \mathrm{d} t+g(t) \mathrm{d} \boldsymbol{w} \Longleftrightarrow \boldsymbol{x}_{t+\Delta t}=\boldsymbol{x}_t+\underbrace{\boldsymbol{f}_t\left(\boldsymbol{x}_t\right) \Delta t}_{\text {确定部分 }}+\underbrace{g_t \sqrt{\Delta t} \boldsymbol{\varepsilon}}_{\text {随机部分 }}, \quad \boldsymbol{\varepsilon} \sim \mathcal{N}(\mathbf{0}, \boldsymbol{I}) $$
其中 $f(\cdot)$ 被称为漂移系数 (drift coefficient), $g(t)$ 被称为扩散系数 (diffusion coefficient), $\boldsymbol{w}$ 是一个标准的布朗运动, $\mathrm{d} w$ 就可以被看成是一个白噪声。这个随机微分方程的解就是一组连续的随机变量 ${\boldsymbol{x}(t)}_{t \in[0, T]}$ 。
同时,任何SDE都有相应的反向SDE,其闭合形式由下式给出:
$$ d \boldsymbol{x}=\left[\boldsymbol{f}_t(\boldsymbol{x})-g_t^2 \nabla_{\boldsymbol{x}} \log p_t(\boldsymbol{x})\right] d t+g_t d \boldsymbol{w} $$
因此,DDPM与NSCN中加噪和去噪的过程不就可以看出正向SDE与逆向SDE?

对于 DDPM,前向加噪过程为 $$ x_{t+1}=\sqrt{1-\beta_{t+1}} x_t+\sqrt{\beta_{t+1}} \varepsilon $$
当 $x \rightarrow 0,(1-x)^\alpha \approx 1-\alpha x$, 那么 $$ \begin{aligned} x_{t+\Delta t} & = \sqrt{1-\beta(t+\Delta t) \Delta t} x_t+\sqrt{\beta(t+\Delta t) \Delta t \varepsilon} \\ & \approx\left(1-\frac{1}{2} \beta(t+\Delta t) \Delta t\right) x_t+\sqrt{\beta(t+\Delta t)} \sqrt{\Delta t} \varepsilon \\ & \approx\left(1-\frac{1}{2} \beta(t) \Delta t\right) x_t+\sqrt{\beta(t)} \sqrt{\Delta t \varepsilon} \end{aligned} $$
对比SDE形式, 得出 $$ f\left(x_t, t\right)=-\frac{1}{2} \beta(t) x_t ;\qquad g(t)=\sqrt{\beta(t)} $$
而对于NCSN,前向加噪过程为 $$ x_{t+\Delta t}=x_t+\sqrt{\sigma_{t+\Delta t}^2-\sigma_t^2} \varepsilon $$
那么 $$ \begin{aligned} x_{t+\Delta t} & =x_t+\sqrt{\sigma_{t+\Delta t}^2-\sigma_t^2} \varepsilon \\ & =x_t+\sqrt{\frac{\sigma_{t+\Delta t}^2-\sigma_t^2}{\Delta t}} \sqrt{\Delta t} \varepsilon \\ & =x_t+\sqrt{\frac{\Delta \sigma_t^2}{\Delta t} \sqrt{\Delta t} \varepsilon} \end{aligned} $$
对比SDE形式, 得出 $$ f\left(x_t, t\right)=0 ;\qquad g(t)=\frac{d}{d t} \sigma_t^2 $$
因此,从上面推导可以看出NCSN和DDPM其实只是SDE框架下不同的$f$和$g$。同时,注意到: 对于NCSN我们有 $$ \frac{x_t}{\sqrt{1+\sigma_t^2}}=\frac{x_0}{\sqrt{1+\sigma_t^2}}+\frac{\sigma_t}{\sqrt{1+\sigma_t^2}} \varepsilon $$
令 $$ \mathrm{x}_t=\frac{x_t}{\sqrt{1+\sigma_t^2}} ; \sqrt{\bar{\alpha}_t}=\frac{1}{\sqrt{1+\sigma_t^2}} $$
可得 $$ \mathrm{x}_t=\sqrt{\bar{\alpha}_t} \mathrm{x}_0+\sqrt{1-\bar{\alpha}_t} \varepsilon $$
可以看出这跟DDPM的加噪过程是相同的。最后,在DDPM的前向过程中, 可以表示为 $$ \left.\boldsymbol{x}_t \sim q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_0\right)=\mathcal{N}\left(\boldsymbol{x}_t ; \sqrt{\bar{\alpha}_t} \boldsymbol{x}_0,\left(1-\bar{\alpha}_t\right) \mathbf{I}\right)\right) $$
对于一个高斯变量 $z \sim \mathcal{N}\left(z ; \mu_z, \Sigma_z\right)$, 有如下结论: $$ \mu_z=z+\Sigma_z \nabla \log p(z) $$
两式带入一下可得 $$ \sqrt{\bar{\alpha}_t} \boldsymbol{x}_0=\boldsymbol{x}_t+\left(1-\bar{\alpha}_t\right) \nabla \log p\left(\boldsymbol{x}_t\right) $$ $\boldsymbol{x}_t=\sqrt{\bar{\alpha}_t} \boldsymbol{x}_0+\sqrt{1-\bar{\alpha}_t} \varepsilon_t$, 因此 $$ \begin{aligned} \boldsymbol{x}_0 & =\frac{\boldsymbol{x}_t+\left(1-\bar{\alpha}_t\right) \nabla \log p\left(\boldsymbol{x}_t\right)}{\sqrt{\bar{\alpha}_t}}=\frac{\boldsymbol{x}_t-\sqrt{1-\bar{\alpha}_t} \varepsilon_t}{\sqrt{\bar{\alpha}_t}} \\ & \Rightarrow \nabla \log p\left(\boldsymbol{x}_t\right)=-\frac{\boldsymbol{\varepsilon}_t}{\sqrt{1-\bar{\alpha}_t}} \end{aligned} $$
因此DDPM去噪过程中预测的是噪声 $\varepsilon_t$, 而噪声正好就是分数的线性关系且方向相反。去噪的过程也就是朝分数方向移动的过程。
参考文献
- https://zhuanlan.zhihu.com/p/662786209
- https://yinglinzheng.github.io/diffusion-model-tutorial/
- https://zhuanlan.zhihu.com/p/658549707
- https://kexue.fm/archives/9119#%E8%AF%A5%E6%80%8E%E4%B9%88%E6%8B%86
- https://zhuanlan.zhihu.com/p/651528231
- https://zhuanlan.zhihu.com/p/595866176
- Ho, J., Jain, A., & Abbeel, P. (2020). Denoising diffusion probabilistic models. Advances in neural information processing systems, 33, 6840-6851.
- Song, Y., & Ermon, S. (2019). Generative modeling by estimating gradients of the data distribution. Advances in neural information processing systems, 32.
- Song, Y., Sohl-Dickstein, J., Kingma, D. P., Kumar, A., Ermon, S., & Poole, B. (2020). Score-based generative modeling through stochastic differential equations. arXiv preprint arXiv:2011.13456.
- Welling, M., & Teh, Y. W. (2011). Bayesian learning via stochastic gradient Langevin dynamics. In Proceedings of the 28th international conference on machine learning (ICML-11) (pp. 681-688).
- Luo, C. (2022). Understanding diffusion models: A unified perspective. arXiv preprint arXiv:2208.11970.