混合高斯模型的代码实现
利用Python和R实现混合高斯模型
Table of Contents
一、生成混合高斯数据
1、原理
利用混合高斯模型的公式:
$$ P(y \mid \theta)=\sum_{k=1}^{K} \alpha_{k} \phi\left(y \mid \theta_{k}\right) $$
只需要给定:
- 各组分布的均值向量及协方差矩阵$\theta_k = \left(\mu_k, \Sigma_k \right)$
- 需要生成的数据总数$N$以及各组权重$\alpha = (\alpha_1,\ldots,\alpha_K)$ 即可生成GMM数据
注意:$\Sigma_k$需要是一个对称正定的矩阵
两种思路:
思路一
- 利用权重$\alpha = (\alpha_1,\ldots,\alpha_K)$进行带权重的抽样,从$[1,2,\ldots,K]$中抽样$N$次得到一个长度为$N$的列表(向量),记为
group_list,第$i$个元素表示数据应该从第$i$个分模型中生成 - 遍历列表(向量)
group_list中的每个元素,若第$i$次遍历中,group_list[i]=k,则表示从$\mathcal{N}(\mu_k,\Sigma_k)$中生成一个数据$X_i$ - 将$X_1,\ldots,X_N$排列合并得到一个矩阵$X=(X_1,\ldots,X_N)$
思路二
- 利用$\alpha = (\alpha_1,\ldots,\alpha_K)$,乘上总数$N$,得到每个类别大致的数量,记为
group_num_list,第$k$个元素表示有group_num_list[k]个数据来源于第$k$个分模型 - 遍历列表(向量)
group_num_list,若在第$k$次遍历中,group_num_list[k]=$n_k$,则表示从$\mathcal{N}(\mu_k,\Sigma_k)$中独立生成$n_k$个数据$X^k=(X_1,\ldots,X_{n_k})$ - 将$X^1,\ldots,X^k$合并得到矩阵$X=(X_1,\ldots,X_N)$
注意:思路一的方法是严格按照GMM的定理来生成的,复杂度为$O(N)$;思路二严格来说与理论有少许差异,但是时间复杂度会低一些,为$O(K)$
2、Python实现
def generate_gmm_data(self, shuffle=True):
"""
:return: 返回一个自变量矩阵X_mat以及一个因变量向量y_vec
"""
assert len(self.weight_vec) == self.K # 判断类别数量是否等于参数的数量
num_list = [int(self.total_num * self.weight_vec[k]) for k in range(self.K)]
if sum(num_list) != self.total_num:
num_list[self.K] += self.total_num - sum(num_list) # 取整后可能存在加和与总数不等的情况,考虑在最后一个组上做处理
assert sum(num_list) == self.total_num
for k in range(self.K):
if len(self.mean_list[k]) > 1:
X_mat_k = np.random.multivariate_normal(self.mean_list[k], self.cov_mat_list[k], num_list[k])
else:
X_mat_k = np.random.normal(self.mean_list[k], self.cov_mat_list[k], num_list[k]).reshape(
(num_list[k], -1))
y_vec_k = np.array([k for _ in range(num_list[k])])
if not k:
X_mat = X_mat_k
y_vec = y_vec_k
else:
X_mat = np.vstack((X_mat, X_mat_k))
y_vec = np.hstack((y_vec, y_vec_k))
if shuffle:
shuffle_index = [x for x in range(self.total_num)]
random.shuffle(shuffle_index)
X_mat = X_mat[shuffle_index]
# if len(X_mat.shape) == 3:
# X_mat = X_mat[0] # 维度为1的情况会升维
y_vec = y_vec[shuffle_index]
self.data = X_mat
self.y_vec = y_vec
3、R实现
generate_gmm_data <- function (params_list=NULL, shuffle=TRUE) {
# params_list是一个list类型,应当包含以下几个数据
# total_num: 需要生成数据的数量
# weight_vec: 各类别的权重
# mean_list: 均值列表
# cov_mat_list: 协方差矩阵列表
if (is.list(params_list)) {
weight_vec <- params_list$weight_vec
total_num <- params_list$total_num
mean_list <- params_list$mean_list
cov_mat_list <- params_list$cov_mat_list
cluster_num <- length(weight_vec)
} else {
# 如果没有给定参数列表,则使用默认设置
weight_vec <- c(0.3, 0.3, 0.4)
total_num <- 100
mean_list <- list(c(-0.5), c(0.5), c(0))
cov_mat_list <- list(matrix(1), matrix(1), matrix(1))
cluster_num <- 3
print("hhh")
}
# 判断cluster数量与mean_list和cov_mat_list中元素个数是否相等
if (length(weight_vec) != cluster_num) {
stop("The length of weight vector is not equal to number of cluster")
}
if (length(mean_list) != cluster_num) {
stop("The length of mean list is not equal to number of cluster")
}
if (length(cov_mat_list) != cluster_num) {
stop("The length of covariance matrix list is not equal to number of cluster")
}
# 各类别的数量
num_before_k <- 0
for (k in 1:cluster_num) {
if (k < cluster_num) {
num_k <- floor(weight_vec[k] * total_num) # 采用向下取整的策略,并在最后一组做处理
num_before_k <- num_before_k + num_k
} else {
num_k <- total_num - num_before_k
}
X_mat_k <- rmvnorm(num_k, mean_list[[k]], cov_mat_list[[k]]) # 生成一个num_k * p 维的matrix
y_vec_k <- rep(k, num_k)
if (k == 1) {
X_mat <- X_mat_k
y_vec <- y_vec_k
} else {
# 纵向合并
X_mat <- rbind(X_mat, X_mat_k)
y_vec <- c(y_vec, y_vec_k)
}
}
# shuffle
if (shuffle) {
shuffle_index <- sample(total_num)
X_mat <- X_mat[shuffle_index, ]
y_vec <- y_vec[shuffle_index]
}
# 构造返回结果
res <- list(X_mat=as.matrix(X_mat), y_vec=y_vec)
return(res)
}
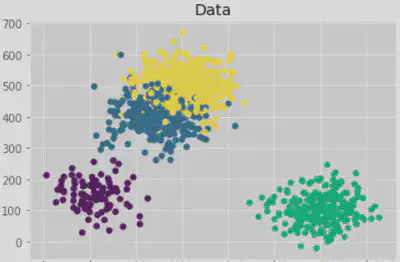
由于GMM类似于聚类模型,因此可以使用Python中Sklearn库中的
make_blobs函数快速生成数据
(X, y) = make_blobs(n_samples=[100,300,250,400], n_features=2,
centers=[[100,150],[250,400], [600,100],[300,500]],
cluster_std=50, random_state=1)
plt.style.use("ggplot")
plt.figure()
plt.title("Data")
plt.scatter(X[:, 0], X[:,1], marker="o", c=np.squeeze(y), s=30)
二、EM算法
1、原理
- GMM的EM实现使用的是传统的EM算法框架,Python实现中,主要使用了
Numpy做矩阵运算,R实现中,其自带的矩阵运算已经能满足要求,不需要另外导包 - 由于EM算法本身是一个迭代求解算法,因此需要给出终止条件,在本文的实现中,使用了两个终止条件:
- 最大迭代次数:
max_iter - 对数似然更新阈值:
eps
- 最大迭代次数:
print_log参数用于控制是否输出每次迭代的信息
思路
-
首先进行初始化,即初始化$\alpha_k$、$\mu_k$、$\Sigma_k$;可以采取多种初始化方法:
- kmeans方法(第三方包常用)
- $\alpha_k$初始化为$\frac{1}{K}$,$\mu_k$选择$K$个数据点的值作为初始化的值,$\Sigma_k$可以选择整体的协方差矩阵作为初始化值
-
E-Step:利用下式更新$\Gamma\in \mathbb{R}^{N\times K}$
$$ \widehat{\gamma}_{j k}=\frac{\alpha_{k} \phi\left(y_{j} \mid \theta_{k}\right)}{\sum_{k=1}^{K} \alpha_{k} \phi\left(y_{j} \mid \theta_{k}\right)} $$
- M-Step:利用下式更新待估计的参数
$$ \widehat{\mu}_{k}=\frac{\sum_{j=1}^{N} \widehat{\gamma}_{j k} y_{j}}{\sum_{j=1}^{N} \widehat{y}_{j k}}\quad \widehat{\sigma}_{k}^{2}=\frac{\sum_{j=1}^{N} \widehat{\gamma}_{j k}\left(y_{j}-\mu_{k}\right)^{2}}{\sum_{j=1}^{N} \widehat{\gamma}_{j k}}\quad \widehat{\alpha}_{k}=\frac{\sum_{j=1}^{N} \hat{\gamma}_{j k}}{N} $$
- 重复直到收敛,这里的收敛条件可以是$|\theta^{(i+1)}-\theta^{(i)}|_2 < \epsilon$,也可以是$|L(\theta^{(i+1)})-L(\theta^{(i)})|<\epsilon$
2、Python实现
def em_algorithm(self, eps=1e-3, max_iter=100, print_log=True):
"""
实现EM算法
:return: 返回各组数据的属于每个分类的概率列表
"""
# 初始化
# 各组概率
pi_list = [1 / self.K for _ in range(self.K)]
# 各组均值: 采用随机选择的策略
initial_index = np.random.choice([x for x in range(self.data.shape[0])], self.K, replace=False).tolist()
mean_list = [self.data[x] for x in initial_index]
# 各组协方差
initial_total_cov = np.cov(self.data.T)
cov_mat_list = [initial_total_cov for _ in range(self.K)]
# 其他
diff_loglikelihood = 100
loglikelihood_old = 0
length, dimension = np.shape(self.data)
# 每个个体属于哪个组
gamma_mat = np.zeros((length, self.K))
# 迭代求解
step = 0
while (abs(diff_loglikelihood) > eps) & (step < max_iter):
# E-Step
for index in range(length):
# 对于每个个体,计算其属于第k个组的概率
gamma_mat[index, :] = [
pi_list[k] * multivariate_normal.pdf(self.data[index], mean_list[k], cov_mat_list[k]) for k in
range(self.K)]
gamma_mat[index, :] = gamma_mat[index, :] / np.sum(gamma_mat[index, :]) # 归一化
# M-Step
gamma_k_list = np.sum(gamma_mat, axis=0).tolist() # 列求和, 得到每个组的gamma求和, size=K
for k in range(self.K):
# 更新均值
mean_list[k] = np.sum(self.data * gamma_mat[:, k].reshape(-1, 1), axis=0) / gamma_k_list[k]
# 更新协方差矩阵
e_mat = self.data - mean_list[k] # 一个N*p维的矩阵
cov_mat_list[k] = (e_mat.T * gamma_mat[:, k]).dot(e_mat) / gamma_k_list[k]
# 更新权重
pi_list[k] = gamma_k_list[k] / self.data.shape[0]
loglikelihood_new = self.data.shape[0] * np.sum(pi_list * np.log(pi_list)) + \
sum([sum([gamma_mat[index, k] * (multivariate_normal.logpdf(self.data[index], mean_list[k], cov_mat_list[k])) for k in range(self.K)]) for index in range(self.data.shape[0])])
# 更新step和loglikehood
step += 1
diff_loglikelihood = loglikelihood_new - loglikelihood_old
loglikelihood_old = loglikelihood_new
if print_log:
print("-----------------------------------------------")
print("Iteration: {}".format(step))
print("Loglikehood Diff: {}".format(diff_loglikelihood))
if print_log:
print("============================================")
print("Total Iteration: {}".format(step))
self.prediction = np.argmax(gamma_mat, axis=1).tolist()
self.mean_prediction = mean_list
self.cov_mat_prediction = cov_mat_list
self.pi_prediction = pi_list
3、R实现
gmm_em_algorithm <- function(data, num_clusters, eps=1e-3, max_iter=100, print_log=TRUE){
# 实现混合高斯的EM算法
# data: N * p维的一个matrix或者dataframe
# num_clusters: 类别数
# eps: 迭代的阈值
# max_iter: 最大迭代次数
# print_log: 每次迭代是否打印日志
data <- as.matrix(data)
total_num <- dim(data)[1]
dimension <- dim(data)[2]
# 初始化
# 各组概率
pi_vec <- rep(1/num_clusters, num_clusters)
# 各组均值: 采用随机选择的策略
initial_index <- sample(total_num, num_clusters)
mean_mat <- data[initial_index, ] # 是一个num_clusters * dimension的矩阵
cov_mat_list <- list()
init_cov_mat <- cov(data)
for (i in 1:num_clusters) {
cov_mat_list[[i]] <- init_cov_mat
}
# 其他
diff_loglikelihood <- 100
loglikelihood_old <- 0
# 每个个体属于哪个组
gamma_mat <- matrix(0, total_num, num_clusters)
# 迭代求解
step <- 0
while ((abs(diff_loglikelihood) > eps) & (step < max_iter)) {
# E-Step
for (index in 1:total_num) {
for (k in 1:num_clusters) {
# 计算第index个个体属于第k个类别的概率
gamma_mat[index, k] <- pi_vec[k] * dmvnorm(x = data[index, ], mean = mean_mat[k, ], sigma = cov_mat_list[[k]])
}
# 归一化
gamma_mat[index, ] <- gamma_mat[index, ] / sum(gamma_mat[index, ])
}
# M-Step
gamma_k_vec <- colSums(gamma_mat) # 列求和, 得到每个组的gamma求和, size=cluster_num
for (k in 1:num_clusters) {
# 更新均值
mean_mat[k, ] <- colSums(data * gamma_mat[, k]) / gamma_k_vec[k]
# 更新协方差矩阵
e_mat <- t(data) - mean_mat[k, ] # 一个dimension * N的矩阵
cov_mat_list[[k]] <- e_mat %*% (t(e_mat) * gamma_mat[, k]) / gamma_k_vec[k]
# 更新权重
pi_vec[k] <- gamma_k_vec[k] / total_num
}
# 计算对数似然
part1 <- total_num * sum(pi_vec * log(pi_vec))
part2 <- 0
for (k in 1:num_clusters) {
# print(cov_mat_list[[k]])
part2 <- part2 + sum(gamma_mat[, k] * dmvnorm(data, mean_mat[k, ], cov_mat_list[[k]]))
}
loglikelihood_new <- part1 + part2
# 更新step和loglikehood
step <- step + 1
diff_loglikelihood <- loglikelihood_new - loglikelihood_old
loglikelihood_old <- loglikelihood_new
if (print_log) {
print("-----------------------------------------------")
print(paste0("Iteration: ", as.character(step)))
print(paste0("Loglikehood Diff: ", as.character(diff_loglikelihood)))
}
}
if (print_log) {
print("============================================")
print(paste0("Total Iteration: ", as.character(step)))
}
# 输出结果
colnames(gamma_mat) <- 1:num_clusters
res <- list(
weight_pred = pi_vec,
mean_pred = mean_mat,
cov_mat_pred = cov_mat_list,
label_pred = as.numeric(apply(gamma_mat, 1, function(t) colnames(gamma_mat)[which.max(t)]))
)
}
4、第三方工具库
在Python中,Sklearn库实现了GMM,R中,mclust包也实现了GMM;调用非常简单
- Sklearn: (API Reference)
from sklearn import mixture
clf = mixture.GaussianMixture(n_components=K, covariance_type='full') # K为类别数
clf.fit(data) # data为需要拟合的数据
- mclust: (API Reference)
# 构建EM算法模型,指定分K类
> EM_model <- Mclust(data = data, G=K) # data为需要拟合的数据
# 查看基本信息
> summary(EM_model)
三、真实数据
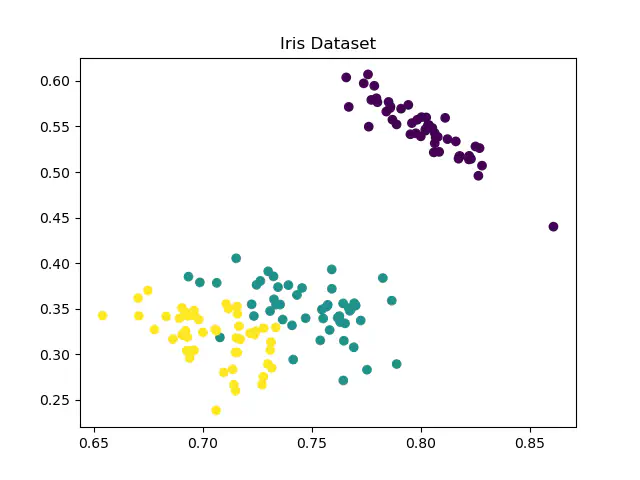
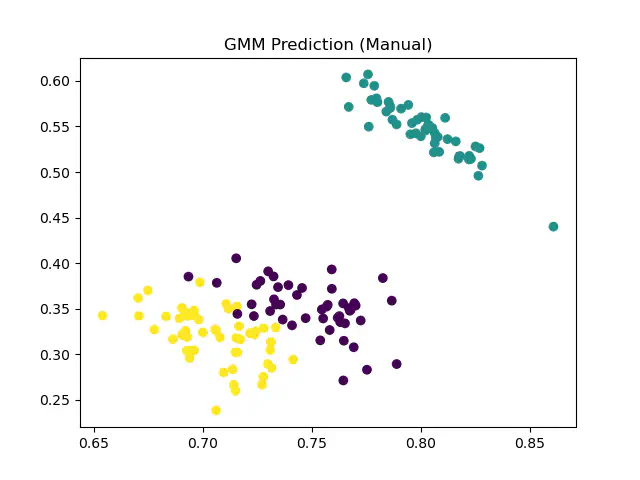
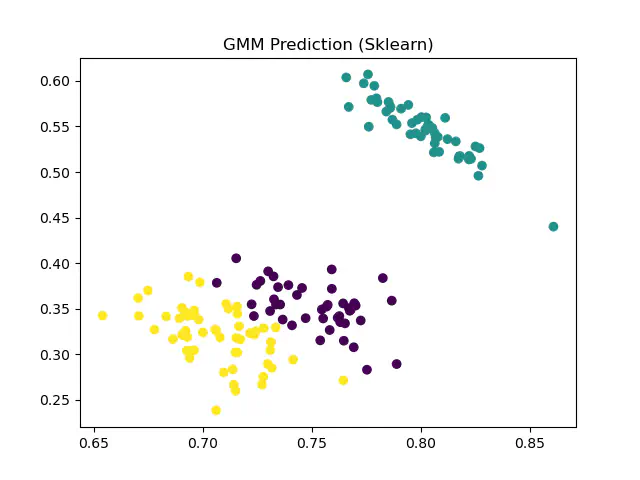
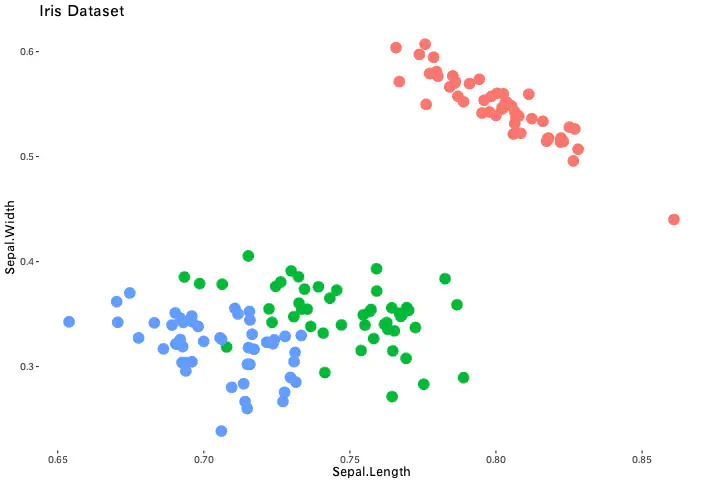
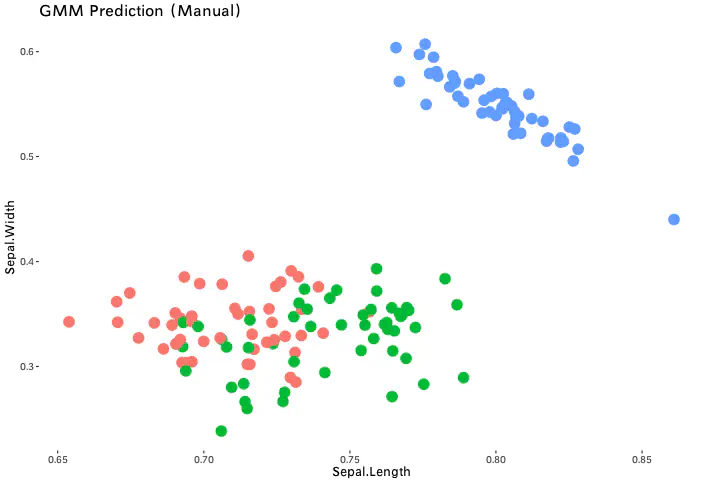
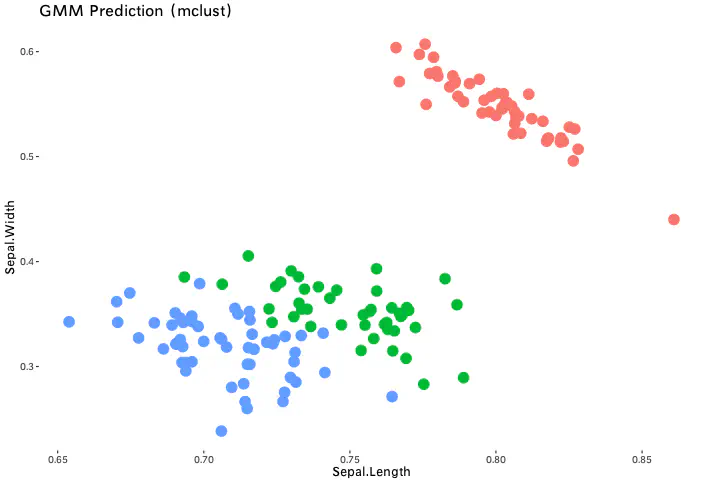
我们使用常用的Iris数据集,分别在R、Python上实现并比较手动实现与第三方工具库实现
1、Python实现
- 手动实现准确率:97.33%
- Sklearn实现准确率:96.67%
2、R实现
- 手动实现准确率:80%
- mclust实现准确率:96.67%
四、后记
手动实现的代码虽能较好实现所需功能,但相较而言没有第三方工具库实现的稳定性高,运行速度上也相差很大;可以进一步探究第三方包在实现上采用了哪些技巧?