KAN: Kolmogorov–Arnold Networks

Zhe Li
May 12, 2024 3 min read Neural Network
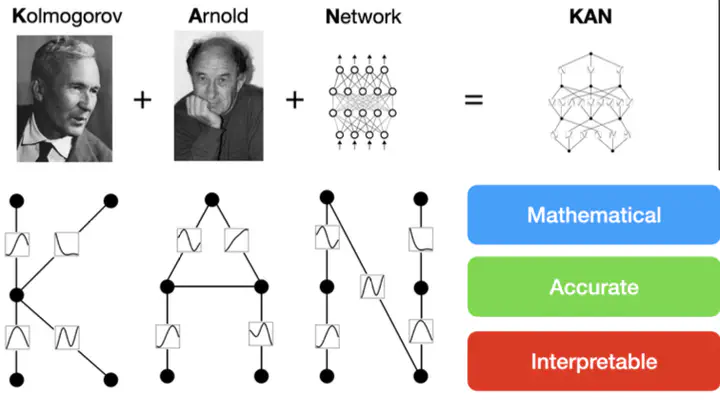
Table of Contents

0、MLP

感知机最早由Rosenblatt于1957年提出，由于其简单的结构而得到快速的发展，下图是一个MLP的示意图

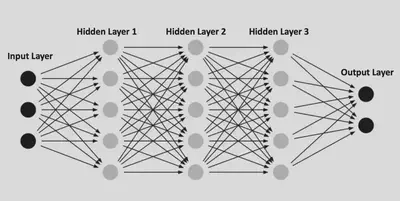
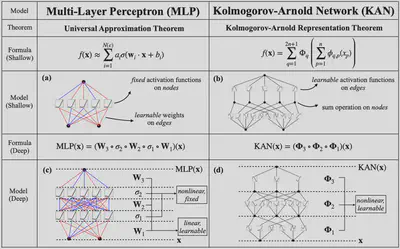
我们可以把上面这个 MLP 表示为： $$ f_{\mathrm{MLP}}(\mathbf{x})=\mathbf{W}_4 \boldsymbol{\sigma}\left(\mathbf{W}_3 \boldsymbol{\sigma}\left(\mathbf{W}_2 \boldsymbol{\sigma}\left(\mathbf{W}_1 \mathbf{x}+\mathbf{b}_1\right)+\mathbf{b}_2\right)+\mathbf{b}_3\right)+\mathbf{b}_4, $$ 可以看出，在 MLP 中，激活函数$\boldsymbol{\sigma}(\cdot)$是作用在节点（node）上的，而边（edge）的连接没有附带任何信息，唯一的作用就是把两层中的所有节点连接起来。

MLP具有很强的拟合能力，常见的连续非线性函数都可以用MLP来近似

但是，我们是否可以把非线性的激活函数放到边上呢？这就是 KAN 的基本思想

一、Kolmogorov–Arnold Networks

1. Kolmogorov-Arnold Representation theorem

Vladimir Arnold与Andrey Kolmogorov证明：如果$f: [0,1]^n \rightarrow \mathbb{R}$是一个多元连续函数，则$f$可以被写成单变量连续函数和加法的有限组合。具体而言， $$ f(\mathbf{x})=f\left(x_1, \ldots, x_n\right)=\sum_{q=1}^{2 n+1} \Phi_q\left(\sum_{p=1}^n \phi_{q, p}\left(x_p\right)\right) . $$ 其中，$\phi_{q, p}:[0,1] \rightarrow \mathbb{R}$，$\Phi_q: \mathbb{R} \rightarrow \mathbb{R}$。

似乎这个理论告诉我们学习一个高维函数归结为学习多项式个一维函数。然而，这些一维函数可能是非光滑甚至是分形的，因此在实践中可能无法学习到。由于这种病态行为，KA表示定理在机器学习中基本上被判了死刑，被认为在理论上是正确的但在实践中无用

2. KAN Architecture

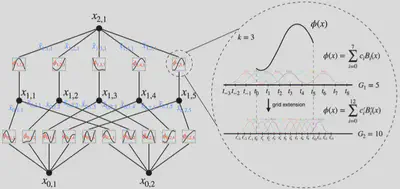
根据KA表示定理，我们只需要找到合适的$\phi_{p,q}$和$\Phi_q$函数，因此可以设计上图这样的一个神经网络，其中$\phi_{p,q}$和$\Phi_q$均为B样条函数。

  • 所以本质上，KA表示定理其实就是一个两层的KAN，但是如何才能像MLP一样把KAN也做深一些呢？

  • 我们首先用$n_i$表示第$i$层的节点数量，定义第$l$层的第$i$个节点的激活值为$x_{l,i}$，在第$l$层与$l+1$层共有$n_ln_{l+1}$个激活函数，我们定义连接$(l,i)$这个节点与$(l+1,j)$这个节点的激活函数为 $$ \phi_{l, j, i}, \quad l=0, \cdots, L-1, \quad i=1, \cdots, n_l, \quad j=1, \cdots, n_{l+1} . $$ 这样就有 $$ \mathbf{x}_{l+1}\in\mathbb{R}^{n_{l+1}}=\underbrace{\left(\begin{array}{cccc} \phi_{l, 1,1}(\cdot) & \phi_{l, 1,2}(\cdot) & \cdots & \phi_{l, 1, n_l}(\cdot) \\ \phi_{l, 2,1}(\cdot) & \phi_{l, 2,2}(\cdot) & \cdots & \phi_{l, 2, n_l}(\cdot) \\ \vdots & \vdots & & \vdots \\ \phi_{l, n_{l+1}, 1}(\cdot) & \phi_{l, n_{l+1}, 2}(\cdot) & \cdots & \phi_{l, n_{l+1}, n_l}(\cdot) \end{array}\right)}_{\boldsymbol{\Phi}_l\in\mathbb{R}^{n_{l+1}\times n_l}} \mathbf{x}_l \in \mathbb{R}^{n_l}, $$ $\boldsymbol{\Phi}_l$相当于是第$l$层 KAN 的函数矩阵，因此一个$L$层的KAN就可以表示为

$$ \operatorname{KAN}(\mathbf{x})=\left(\boldsymbol{\Phi}_{L-1} \circ \boldsymbol{\Phi}_{L-2} \circ \cdots \circ \boldsymbol{\Phi}_1 \circ \boldsymbol{\Phi}_0\right) \mathbf{x} $$ 对比 MLP： $$ \operatorname{MLP}(\mathbf{x})=\left(\mathbf{W}_{L-1} \circ \sigma \circ \mathbf{W}_{L-2} \circ \sigma \circ \cdots \circ \mathbf{W}_1 \circ \sigma \circ \mathbf{W}_0\right) \mathbf{x} . $$ 可以看出，MLP将线性变换与非线性激活分别用$\mathbf{W}$和$\sigma$实现，而KAN直接在$\boldsymbol{\Phi}_l$中实现了线性变换和非线性激活

3. KAN’s Approximation Abilities and Scaling Laws

Theorem 2.1 (Approximation theory, KAT). Let $\mathbf{x}=\left(x_1, x_2, \cdots, x_n\right)$. Suppose that a function $f(\mathbf{x})$ admits a representation $$ f=\left(\boldsymbol{\Phi}_{L-1} \circ \boldsymbol{\Phi}_{L-2} \circ \cdots \circ \boldsymbol{\Phi}_1 \circ \boldsymbol{\Phi}_0\right) \mathbf{x} $$ as in Eq. (2.7), where each one of the $\Phi_{l, i, j}$ are $(k+1)$-times continuously differentiable. Then there exists a constant $C$ depending on $f$ and its representation, such that we have the following approximation bound in terms of the grid size $G$ : there exist $k$-th order $B$-spline functions $\Phi_{l, i, j}^G$ such that for any $0 \leq m \leq k$, we have the bound $$ \left\|f-\left(\boldsymbol{\Phi}_{L-1}^G \circ \boldsymbol{\Phi}_{L-2}^G \circ \cdots \circ \boldsymbol{\Phi}_1^G \circ \boldsymbol{\Phi}_0^G\right) \mathbf{x}\right\|_{C^m} \leq C G^{-k-1+m} . $$

Here we adopt the notation of $C^m$-norm measuring the magnitude of derivatives up to order $m$ : $$ \|g\|_{C^m}=\max _{|\beta| \leq m} \sup _{x \in[0,1]^n}\left|D^\beta g(x)\right| . $$

从结果来看，KAN的 upper bound 与维度$n$无关，破除了“维数诅咒”，从统计的角度开本质上就是引入了``可加结构’’，使得每个节点类似于一维的速度

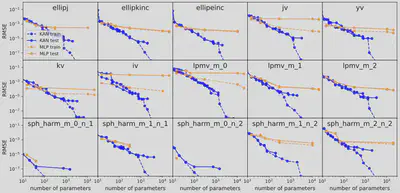
  • Neural scaling laws: comparison to other theories：神经缩放定律描述了测试损失随着模型参数增加而减少的现象，即 $\ell \propto N^{-\alpha}$，其中 $\ell$ 表示测试均方根误差 (RMSE)，$N$ 为参数数量，$\alpha$ 为缩放指数。较大的 $\alpha$意味着通过简单地扩展模型可以获得更多的改进

    • Sharma 和 Kaplan 提出$\alpha$与输入流形维度$d$相关，如果模型函数类是阶数为$k$的分段多项式（对于 ReLU，$k=1$），那么标准逼近理论暗示$\alpha = \frac{k+1}{d}$。这一界限受限于维度诅咒。Michaud 等人考虑了仅涉及一元（例如，平方、正弦、指数）和二元（加法和乘法）运算的计算图，发现 $\alpha = \frac{k+1}{d^*} = \frac{k+1}{2}$，其中 $d^* = 2$ 是最大元数。

    • KAN假设存在平滑的 Kolmogorov-Arnold 表示，将高维函数分解为若干一维函数，得出 $\alpha = k+1$（其中 $k$ 是分段多项式样条的阶数）。如果选择 $k=3$ 的三次样条，因此 $\alpha=4$。

  • Comparison between KAT and UAT：全连接神经网络的强大功能由普适逼近定理（Universal Approximation Theorem, UAT）证明，该定理表明，给定一个函数和误差容忍度 $\epsilon > 0$，一个具有 $k > N(\epsilon)$ 个神经元的两层网络可以在误差 $\epsilon$ 范围内逼近该函数。然而，UAT 并未保证 $N(\epsilon)$ 如何随 $\epsilon$ 缩放的界限。实际上，它受制于维度诅咒（COD），并且在某些情况下 $N$ 被证明会随着 $d$ 指数级增长 [15]。KAT 和 UAT 之间的区别在于，KANs 利用了函数的内在低维表示，而 MLPs 则没有。

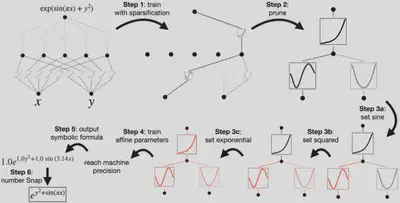
4. For Interpretability: Simplifying KANs and Making them interactive

如果我们需要拟合函数$f(x,y)=\exp\big(\sin(\pi x)+y^2\big)$，那么用$[2,1,1]$这个结构的 KAN 是最合适的，但是我们无法提前知道函数的形式，应该如何与 KAN 交互得到我们想要的结构呢？

首先定义一个有$N_p$输入的激活函数$\phi$的$L_1$范数：

$$ |\phi|_1 \equiv \frac{1}{N_p} \sum_{s=1}^{N_p}\left|\phi\left(x^{(s)}\right)\right| . $$

因此，对于一个$n_{\text {in }}$输入$n_{\text {out }}$输出的 KAN 层，定义$L_1$范数为

$$ |\boldsymbol{\Phi}|_1 \equiv \sum_{i=1}^{n_{\text {in }}} \sum_{j=1}^{n_{\text {out }}}\left|\phi_{i, j}\right|_1 $$

定义$\Phi$的交叉熵为

$$ S(\boldsymbol{\Phi}) \equiv-\sum_{i=1}^{n_{\text {in }}} \sum_{j=1}^{n_{\text {out }}} \frac{\left|\phi_{i, j}\right|_1}{|\boldsymbol{\Phi}|_1} \log \left(\frac{\left|\phi_{i, j}\right|_1}{|\boldsymbol{\Phi}|_1}\right) $$

因此，损失函数$\ell_{\text {total }}$表示为：

$$ \ell_{\text {total }}=\ell_{\text {pred }}+\lambda\left(\mu_1 \sum_{l=0}^{L-1}\left|\boldsymbol{\Phi}_l\right|_1+\mu_2 \sum_{l=0}^{L-1} S\left(\boldsymbol{\Phi}_l\right)\right), $$

Continual Learning

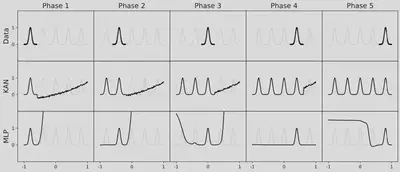
KAN具有局部可塑性，并且通过利用样条的局部性可以避免灾难性遗忘。原因是由于样条基是局部的，一个样本只会影响附近的几个样条系数，远处的系数则保持不变。相反，由于 MLPs 通常使用全局激活函数，例如 ReLU/Tanh/SiLU 等，任何局部变化都可能不受控制地传播到远离的区域，破坏那里存储的信息

Application

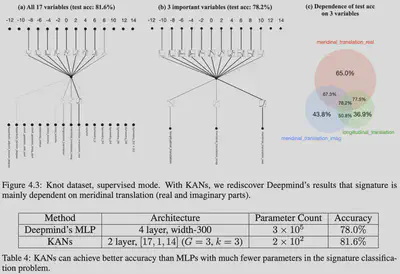
结不变量是用来描述和区分不同结的性质的量，它们是结论中的一种重要概念。结不变量是指那些在结变形时保持不变的特征或量，它们可以帮助我们确定两个结是否同构或等价。结不变量可以是几何特征、代数特征或拓扑特征，常见的包括但不限于Jones多项式、Jones多项式的变种、Alexander多项式、交错数、三色定理等。

在结论中，“signature”（签名）是一个结不变量，它是由代数结论家 John Milnor 在1957年提出的。签名是结的一个数字特征，可以通过对结进行某种标准操作（如连接和平移）得到。签名的概念在结论中有着广泛的应用，并在理解结的性质和关系方面提供了重要的见解。

符号主义 or 连接主义？

KAN 介于符号主义与连接主义之间

MLP 与 KAN 如何选择？

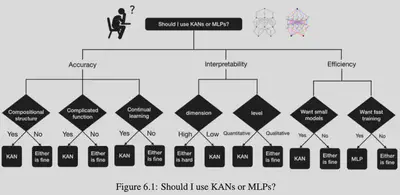
二、KAN 的一些问题

  • 目前在图片分类任务上（例如MNIST数据集）的表现不如MLP
  • KAN的训练速度比 MLP 慢很多
  • 短期看KAN还很难取代MLP，主要原因还是因为KAN的训练算力要求明显高于MLP，想做大模型会有很高的算力壁垒。但是作者强调 KAN 更适用于 AI4Science 的任务，在这样的任务中，不需要这么大的模型，而是更关心收敛的速度

参考文献

B样条 Lagrange插值 贝塞尔曲线