B样条(B-Splines)
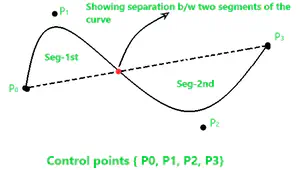
Table of Contents
一、Lagrange插值法
已知若干点,如何得到光滑曲线?是否可以通过在原有数据点上进行点的填充生成曲线?
- 如果知道三个点: $P_0, P_1, P_2$, 如何确定一条曲线 ?
- 想法: 将$P_0, P_1$ 进行连接,然后将$P_1, P_2$ 进行连接,。但是这样的一个曲线并不光滑
- 注意到,直线可以由2个点确定, 而二次曲线由三个点即可确定,推广到一般情况, $n-1$ 阶曲线可以由$n$个点确定
- 这本质上就是Lagrange插值法的思想 (必须经过所有点)
- 一般来说,如果我们有 $n$ 个点 $\left(x_1, y_1\right), \ldots,\left(x_n, y_n\right)$ ,各 $x_i$ 互不相同。对于 1 到 $\mathrm{n}$ 之间的每个 $k$, 定义 $n-1$ 次多项式 $$ L_k(x)=\frac{\left(x-x_1\right) \ldots\left(x-x_{k-1}\right)\left(x-x_{k+1}\right) \ldots\left(x-x_n\right)}{\left(x_k-x_1\right) \ldots\left(x_k-x_{k-1}\right)\left(x_k-x_{k+1}\right) \ldots\left(x_k-x_n\right)} $$
- $L_k(x)$ 具有有趣的性质: $L_k\left(x_k\right)=1, L_k\left(x_j\right)=0, j \neq k$. 然后定义一个 $n-1$ 次多项式 $$ P_{n-1}(x)=y_1 L_1(x)+\ldots+y_n L_n(x)=\sum_{i=1}^ny_iL_i(x) . $$ 这样的多项式 $P_{n-1}(x)$ 满足 $P_{n-1}\left(x_i\right)=y_i, i=1,2, \ldots, n$. 因此必过控制点$\{(x_i,y_i)\mid i=1,\ldots,n\}$;这就是著名的拉格朗日插值多项式!
- 我们可以把$L_1(x),\ldots,L_n(x)$看作基函数,而Lagrange插值本质上就是一组基的线性组合!
Lagrange插值法例子
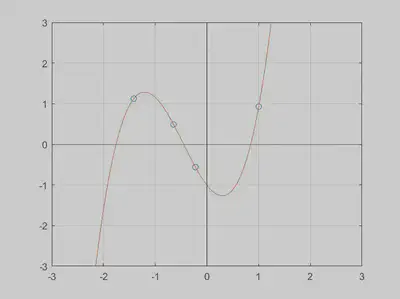
- 已知区间 $[-1,1]$ 上函数 $f(x)=[1+(5 x)^2]^{-1}$。取等距节点 $$ x_i=-1+\frac{i}{5}, \quad i=0,1,2, \cdots, 10 $$
- 作Lagrange插值多项式
$$
P_{10}(x)=\sum_{i=0}^{10} f\left(x_i\right) L_i(x) .
$$
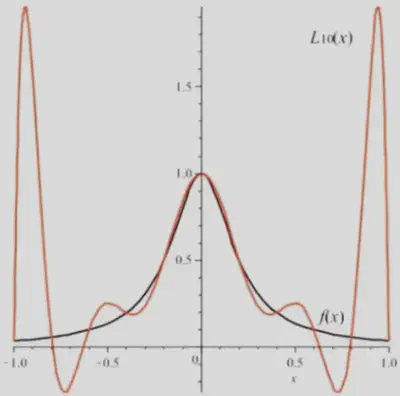
Runge现象出现的原因是在因为在进行Lagrange插值时要求必须要过控制点,因此可以考虑不过控制点进行插值,这样就能避免Runge现象
- 插值法因为要求经过所有节点, 所以导致这种结果, 因此在此基础上提出了拟合的概念:
- 依据原有数据点,通过参数调整设置,使得生成曲线与原有点差距最小 (最小二乘), 因此曲线未必会经过原有数据点
- 样条曲线 (Spline curves): 是给定一系列控制点而得到的一条曲线,曲线形状由这些控制点控制。一般分为插值样条和拟合样条。

二、(Bezier)贝塞尔曲线与B-Splines
- 均匀节点意义下的一元 B 样条 (B-splines, Basis Splines 缩写)是在 1946 年由 1.J.Schoenberg 提出
- 1962 年, 法国数学家 Pierre Bezier 研究了一种曲线, 即 Bezier 曲线
- 1972 年, de Boor 与 cox 分别独立提出了计算 B 样条基函数的公式这个公式对 B 样条作为计算机辅助几何设计 (CAGD)重要工具起到了至关重要的作用,称之为 de Boor-Cox 公式,即著名的 de Boor 算法
1、(Bezier)贝塞尔曲线
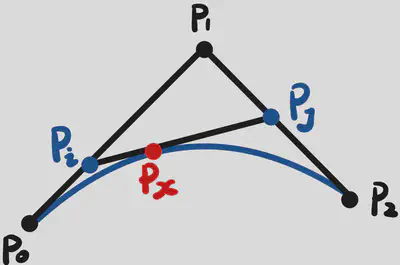
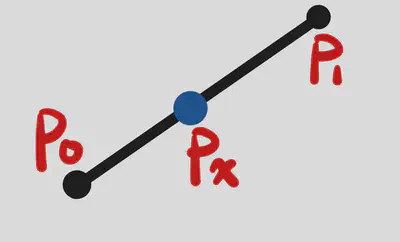
- 不过 $P_1$ : $$ \begin{gathered} P_i&=(1-t) P_0+t P_1 ;\\ P_j&=(1-t) P_1+t P_2 ; \\ P_x&=(1-t) P_i+t P_j. \end{gathered} $$ 其中, $$ \frac{P_0 P_i}{P_0 P_1}=\frac{P_1 P_j}{P_1 P_2}=\frac{P_j P_x}{P_i P_j}=t $$
- 因此我们可以得到:$P_x=\left(1-t^2\right) P_0+2 t(1-t) P_1+t^2 P_2$
- 我们可以把$P_0,P_1,P_2$看作控制点,把$(1-t^2)$,$2t(1-t)$和$t^2$看作是基函数
- 推广到一般情况,假设一共有 $n+1$ 个点, 就可以确定了$n$次的贝塞尔曲线 $$ B(t)=\sum_{i=0}^n C_n^i(1-t)^{n-i} t^i P_i, \quad t \in[0,1] $$
- 或者写成这样 $$ B(t)=W_{t, n}^0 P_0+W_{t, n}^1 P_1+\cdots+W_{t, n}^n P_n $$
- 可以理解为以$W$为基, $P$为系数的线性组合;其中$W_i=C_n^i(1-t)^{n-i} t^i$
注:当有$n+1$个点, 有$n+1$个基函数, 确定$n$阶函数曲线
-
$W_{t, n}^i$为$P_i$的系数, 是最高幂次为$n$的关于$t$的多项式。当 $t$确定后, 该值就为定值。
-
因此整个式子可以理解为$B(t)$插值点是这$n+1$个点施加各自的权重$W$后累加得到的。这也是为什么改变其中一个控制点, 整个贝塞尔曲线都会受到影响。
-
其实对于样条曲线的生成,本质上就对于各个控制点施加权重
-
$n$阶贝塞尔曲线$B^n(t)$可以由前$n$个点决定的$n-1$次贝塞尔曲线$B^{n-1}\left(t \mid P_0, \cdots, P_{n-1}\right)$与后$n$个点决定的$n-1$次贝塞尔曲线$B^{n-1}\left(t \mid P_1, \cdots, P_n\right)$线性组合递推而来,即 $$ {\color{red} \begin{aligned} & B^n\left(t \mid P_0, P_1, \cdots, P_n\right)= \\ & (1-t) B^{n-1}\left(t \mid P_0, P_1, \cdots, P_{n-1}\right)+t B^{n-1}\left(t \mid P_1, P_2, \cdots, P_n\right) \end{aligned} } $$
2、B-Splines
- 我们比较好奇的是对于B样条,怎么得到各控制点前的权重(基函数)
- B-Splines的一些重要定义:
- 控制点: 控制曲线的点, 等价于贝塞尔函数的控制点, 通过控制点可以控制曲线形状。假设有 $n+1$ 个控制点 $P_0, P_1, \ldots, P_n$ 。
- 节点: 与控制点无关,是人为地将目标曲线分为若干个部分,其目的就是尽量使得各个部分有所影响但也有一定独立性,这也是为什么 $\mathrm{B}$ 样条中, 有时一个控制点的改变, 不会很大影响到整条曲线,而只影响到局部的原因,这区别于贝塞尔曲线。
- 节点划分影响权重计算,假设我们划分 $m+1$ 个节点 $t_0, t_1, \ldots, t_m$ ,将曲线分成了 $m$ 段。
- 次 (degree) 与阶 (order): 次的概念是贝塞尔中次的概念, 即权重中$t$的最高幂次。阶 (order) $=$ 次 (degree) +1 。通常我们用 $k$ 表示次。
- 注意到: $$ B(t)=\sum_{i=0}^n W_i P_i=\sum_{i=0}^n B_{i, k}(t) P_i $$ 我们需要获得$W_i$即可。$W_i$是关于$t$的函数, 最高幂次为$k$。$B$样条中通常记为$B_{i, k}(t)$, 即表示第$i$点的权重, 是关于$t$的函数,且最高幂次为$k$。而这个权重函数$B_{i, k}(t)$,在 B样条里叫做$k$次B样条基函数
- $B_{i, k}(t)$ 满足如下递推式 (de Boor 递推式) $$ {\color{blue} \begin{gathered} k=0, \quad B_{i, 0}(t)= \begin{cases}1, & t \in\left[t_i, t_{i+1}\right] \\ 0, & \text { Otherwise }\end{cases} \\ k>0, \quad B_{i, k}(t)=\frac{t-t_i}{t_{i+k}-t_i} B_{i, k-1}(t)+\frac{t_{i+k+1}-t}{t_{i+k+1}-t_{i+1}} B_{i+1, k-1}(t) \end{gathered} } $$
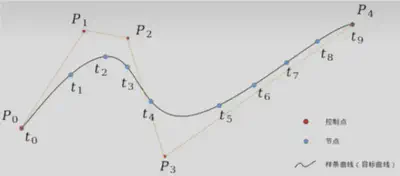
节点数、控制点数与次数的关系
- 控制点有$n+1=5$个, $n=4$ ,即 $P_0, P_1, P_2, P_3, P_4$
- 节点规定为 $m+1=10$ 个, $m=9$ ,即 $t_0, t_1, \cdots, t_9$ ,该节点将要生成的目标曲线分为了 9 份,
- 这里的 $t$ 取值一般为 $0-1$的一系列非递减数。 $t_0, t_1, \cdots, t_9$ 组成的序列,叫做节点表,如等分的节点表 $\{0, \frac{1}{9}, \frac{2}{9}, \frac{3}{9}, \frac{4}{9}, \frac{5}{9}, \frac{6}{9}, \frac{7}{9}, \frac{8}{9}, 1\}$
- 次为$k$。
- 三者有个必须要满足的关系式为
$$m=n+k+1$$
- 为什么满足$m=n+k+1$?

实例计算
- 节点设置:
- 节点向量: $x=0,0.25,0.5,0.75,1$
- 节点数: $m+1=5(m=4)$
- 节点: $x_0=0, x_1=0.25, x_2=0.5, x_3=0.75, x_4=1$
- 节点区间: $\left[x_0, x_1\right),\left[x_1, x_2\right),\left[x_2, x_3\right),\left[x_3, x_4\right)$
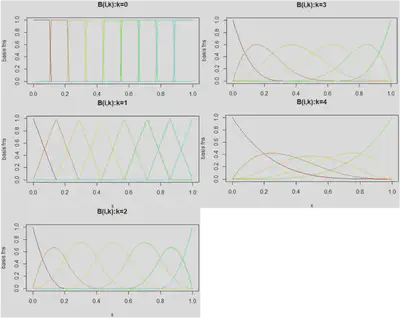
- 0 次 (degree) 基函数为: $$ \begin{aligned} & B_{0,0}(x)=\left\{\begin{array}{lcc} 1 & \text { if } & x_0 \leq x<x_1 \\ 0 & & \text{ other } \end{array}\right. \\ & B_{1,0}(x)=\left\{\begin{array}{ccc} 1 & \text { if } & x_1 \leq x<x_2 \\ 0 & & \text{ other } \end{array}\right.\\ & B_{2,0}(x)=\left\{\begin{array}{ccc} 1 & \text { if } & x_2 \leq x<x_3 \\ 0 & & \text{ other } \end{array}\right.\\ & B_{3,0}(x)=\left\{\begin{array}{ccc} 1 & \text { if } & x_3 \leq x<x_4 \\ 0 & & \text{ other } \end{array}\right.\\ & B_{4,0}(x)=\left\{\begin{array}{ccc} 1 & \text { if } & x_4 \leq x<x_5 \\ 0 & & \text{ other } \end{array}\right. \end{aligned} $$
- 因此由上可知, 0次(degree)基函数均是分段函数
- 基函数的迭代公式: $$ \begin{aligned} & B_{i, k}(x)=\frac{x-x_i}{x_{i+k}-x_i} B_{i, k-1}(x)+\frac{x_{i+k+1}-x}{x_{i+k+1}-x_{i+1}} B_{i+1, k-1}(x) \end{aligned} $$
- $k=1, i=0$时, 一次基函数 $$ \begin{aligned} B_{0,1}(x)&=\frac{x-x_0}{x_1-x_0} B_{0,0}(x)+\frac{x_2-x}{x_2-x_1} B_{1,0}(x)\\ &=4 x B_{0,0}(x)+(2-4 x) B_{1,0}(x) \\ B_{0,1}(x)&=\left\{\begin{array}{cc} 4 x & 0 \leq x<0.25 \\ 2-4 x & 0.25 \leq x<0.5 \\ 0 & \text { other } \end{array}\right. \end{aligned} $$
- 若 $m=4, n=2, k=1$ 基函数 $n+1=3$ 个,基函数次数为 $k=1$
- 若 $m=4, n=1, k=2$ 基函数 $n+1=2$ 个, 基函数次数为 $k=2$

三、样条估计
- 对于多元线性回归,我们有$\widehat{Y}=\mathbf{H}Y$,其中$\mathbf{H}$为帽子矩阵(hat matrix),定义为$\mathbf{H}=X(X^\top X)^{-1}X^\top$
- 对于样条估计,假设模型形式为: $$ \begin{aligned} y&=\beta+\sum_{i=0}^n B_{i, k}(x) \beta_i\\ &=\beta+\beta_0 B_{0, k}(x)+\ldots+\beta_{m-k-1} B_{m-k-1, k}(x) \end{aligned} $$ 其中 $\beta_i$ 是待估参数, $B_{i, k}(x)$ 为样条基函数,此时模型中的基函数个数为 $n=m-k-1$
- 设计矩阵: 设计矩阵 $k=1, n=2, m=4$ :(矩阵的列对应节点区间,相应的区间位置,填入相应的基函数) $$ X=\left[\begin{array}{llll} 1 & B_{01} & B_{11} & B_{21} \\ 1 & B_{01} & B_{11} & B_{21} \\ 1 & B_{01} & B_{11} & B_{21} \\ 1 & B_{01} & B_{11} & B_{21} \end{array}\right]=\left[\begin{array}{cccc} 1 & 4 x & B_{11} & B_{21} \\ 1 & 2-4 x & B_{11} & B_{21} \\ 1 & 0 & B_{11} & B_{21} \\ 1 & 0 & B_{11} & B_{21} \end{array}\right] $$
- 帽子矩阵: $H=X\left(X^T X\right)^{-1} X^T$, 样条估计为: $\hat{y}=H y$
四、拟合样条对深度学习中的双下降(Double Decent)现象的解释
参考 Prof. Daniela Witten发在Twitter上的文章
- Bias-Variance Trade-off ?
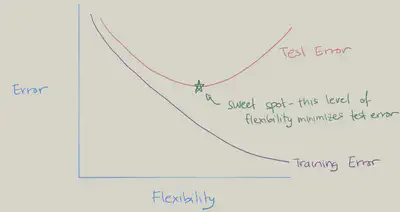
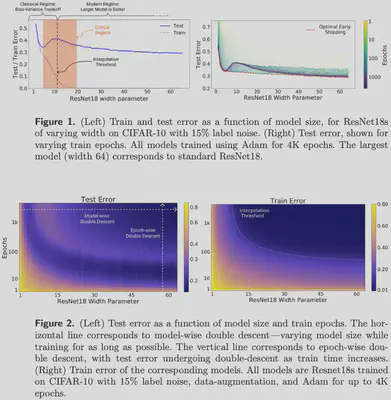
- $\mathrm{U}$型测试误差曲线基于以下公式: $$\text{Exp. Pred. Error} = \text{Irreducible Error}+\operatorname{Bias}^2+ \text{Var}$$
- 随着灵活性的增加, (平方) 偏差减少, 方差增加。sweet spot需要权衡偏差和方差, 即具有中等程度灵活性的模型。
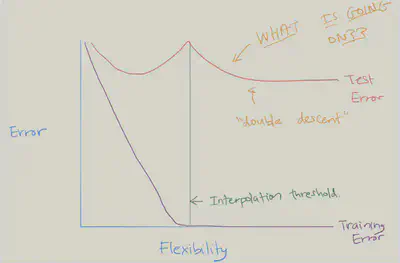
- 过去的几年中,尤其是在深度学习领域,已经出现双下降现象。当你继续拟合越来越灵活且对训练数据进行插值处理的模型时,测试误差会再次减小!
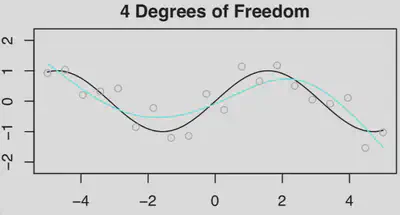
- 考虑自然三次样条曲线(natural cubic spline),拟合模型为$Y=f(x)+\epsilon$,所用基函数的数量与样条曲线的自由度(degrees of freedom, DF)相同。基函数基本形式如下: $$ \left(X-\psi_1\right)_{+}^3,\quad \ldots,\quad\left(X-\psi_K\right)_{+}^3 $$
- 我们首先生成$n=20$组$(X,Y)$数据,首先拟合一个$df=4$的样条曲线【$n=20$ 时的观测值为灰色小圆点,$f(x)=\sin(x)$ 为黑色曲线,拟合函数为浅蓝色曲线。】
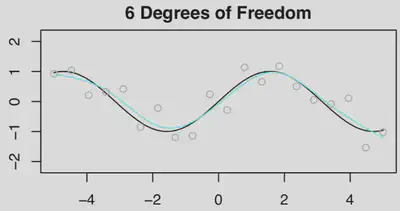
- 然后分别拟合$df=6$和$df=20$的样条曲线
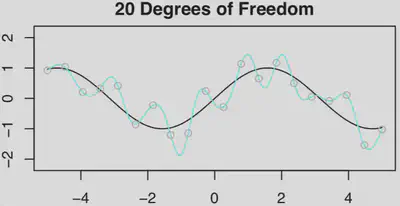
- 如果继续拟合$df=36$($p>n$)的样条曲线,由于解是不唯一的,为了在无穷多个解中进行选择,可以选择范数拟合:系数平方和最小的那个(利用SVD计算)
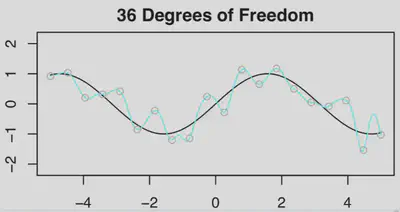
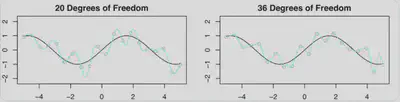
- 对比了$df=20$和$df=36$的结果,可见$df=36$的结果比$df=20$要好一点。这是什么原因呢?
- 下图是训练误差和测试误差曲线,两者的变化曲线差别非常大。以虚线为分界线,当$p>n$时,为什么测试误差(暂时)减少?
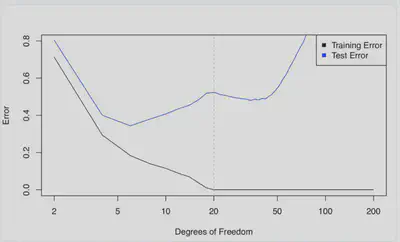
- 一个合理的解释为:关键在于当$df=20$,即$df=n$时,只有一个最小二乘拟合的训练误差为零。这种拟合会出现大量的振荡。
- 但是当增加自由度,使得$p>n$时,则会出现大量的插值最小二乘拟合。最小范数的最小二乘拟合是这无数多个拟合中振荡最小的,甚至比$p=n$时的拟合更稳定。
- 所以,选择最小范数最小二乘拟合实际上意味着$df=36$的样条曲线比$df=20$ 的样条曲线的灵活性差。
- 如果在拟合样条曲线时使用了ridge penalty,而不是最小二乘,结果会怎么样呢?这时将不会有插值训练集,也不会看到双下降,而且会得到更好的测试误差
- 所以,这些与深度学习有何关系?当使用(随机)梯度下降法来拟合神经网络时,实际上是在挑选最小范数解!因此,样条曲线示例非常类似于神经网络双下降时发生的情况。
- 换种说法,当模型能力恰好能够产生零训练误差时,该现象导致测试误差达到峰值。但是,峰值不会出现在多层网络中,因为多层网络在优化时存在隐式正则化的现象